Outreach

Photo credit: © TRIANGEL Transfer | Kultur | Raum, Photo: Sandra Göttisheim

Science is exciting, and it has the power to change the world! But sometimes this is hard to see, when results are written up in papers and hidden behind complicated formulas. I believe that scientific outreach can serve three important purposes:

• Sharing the excitement and wonder of discovery with younger audiences helps to inspire the next generation of scientists.
• Accessible talks on seemingly complicated topics improve our communication skills and foster critical thinking in society.
• Many theoretical physicists (like myself) are publicly funded, and explaining the progress in our work to the general public holds us accountable.

With that in mind, on these pages I want to keep myself accountable and list all efforts to communicate my scientific work to audiences outside of academia. And if you would like me to give a generally accessible talk on black holes, General Relativity, or my work in physics, or take part in an outreach event, please feel free to contact me, and I will do my best to get back to you.

Meet the Institutes!

Every year in spring (this photo is from 2025) KIT hosts the “Meet the Institutes” event, where B.Sc. and M.Sc. students can learn about the research activities in the Department of Physics. I am always eager to participate, because it is a great way to meet new students, and tell them about the work that we do. As an extra motivation you can see “black hole donuts” in the picture below: since the black hole photograph of Messier M87 strikingly resembles a donut, I started the tradition to hand out donuts when we present our black hole group.

Studieninformationstag

Every fall, KIT invites high school students to come visit us, and we put together a one-day program on all the exciting work we do here. Here you can see my colleague Felix Kahlhöfer and myself give a talk on black holes and gravitational waves. The lecture hall was packed almost to the last seat, it was an incredible experience. We even had to end the question period because the next talk was scheduled to start, but there were just too many questions. Many high school students stayed around, and kept talking with us about their plans and dreams and questions about university life, during a few snacks and coffee.

Photo credit: © Torben Ferber

Museum of Natural History Karlsruhe

In fall 2024, I was invited for an evening on “Our Universe” to the Museum of Natural History in Karlsruhe. Together with colleagues from KIT we heard about neutrino particle physics (Dr. Donghwa Kang), their detection and depiction in the arts (Dr. Tim Otto Roth), and I had the opportunity to speak about gravitational waves, and my favorite topic: black holes! There were many questions in a crowded lecture hall, and we all left the evening having felt that we learned something new.

Photo credit: © Beatrix von Puttkamer/KIT

“Today I Learned” Festival: Black Hole Panel Discussion

Organized by TRIANGEL in the summer of 2024, I was part of an exciting panel discussion on black holes. We first watched Peter Galison's The Edge of All We Know (a movie about the first-ever black hole photograph and many other cool black-holey things) and then opened the floor for questions by the public. It was a fantastic evening, and I am grateful I could be part of it!

Photo credit: © TRIANGEL Transfer | Kultur | Raum, Photo: Sandra Göttisheim

Three Minute Thesis (3MT)

In the Three Minute Thesis (3MT) competition, graduate students are challenged to present their work in three minutes to a live audience. It's a little bit like an elevator pitch. In 2019 I was lucky to be one of the ten 3MT finalists at the University of Alberta, and you can find my talk on YouTube. It's titled Black Holes and Einstein's End of Eternity, and it is about the end of space and time that may or may not sit inside black holes.

Veritasium Science Communication Contest

In August 2021, the popular science YouTuber Veritasium held a science communication contest, and this video is my contribution. I talk about what's inside a black hole:

Images of Research

Sometimes, a picture is worth a thousand words. No, really, and that's what the Images of Research Competition at the University of Alberta is all about: to capture your research in one image and share it with the local community as well as online. I have participated in this event three times, and below you can find my contributions:

Back to back

• How do we know the stuff we know?
• In physics and engineering, a lot of our knowledge comes from calculations. And when these calculations become difficult, we need tools to perform them.
• Fifty years ago, mechanical calculators (pictured left) were the tool of choice, and they allowed us to quickly add, subtract, multiply, and divide numbers. They are reliable, make a heck of a noise, weigh 20 pounds, and they just work. They solved many problems before the advent of the computer, contributing a huge amount to what we know today. But as science progressed, new and faster tools were required.
• Today, almost every day, I use my computer (pictured right) to solve the equations I encounter in my research in physics. Don't get me wrong: many of those calculations could, in principle, still be done on the mechanical calculator, but a computer is just faster, quieter, and does not weigh as much.
• In the background you can see a part of the equation that I solved using my computer. Below it, the mechanical calculator and the laptop stand "back to back," as if they are debating who is better at solving it.
• My contribution to the Images of Research Competition 2020 at the University of Alberta, which received a semi-finalist prize.

Solve for x

• This is not just a high school evergreen, but it is vitally important for many applications in research. Recasting an equation into a more convenient form is the most fundamental tool that a theoretical physicist makes use of, every day of every week of every year.
• As it turns out, this is not always possible. Some equations resist even the most sophisticated calculational techniques, which is why they are called "transcendental." But what can we do then? When we encountered such a transcendental equation in our research, we resorted to a graphical method on the computer, and we obtained the graphical shape depicted in this contribution.
• At the bottom right you can see my handwritten original equation. The graphic above shows how we can solve it: wherever the white lines meet, we find a solution of the equation. This is not only important for science, it also gives rise to a beautiful and intricate shape, deeply embedded in the mathematical structure of equations. When I was in highschool, I never thought I would meet an equation like that. Solve for x...
• Based on J.B., V. P. Frolov and A. Zelnikov, “Quantum scattering on a delta potential in ghost-free theory,” Phys. Lett. B 782, 688 (2018); arXiv:1805.01875 [hep-th]. My contribution to the Images of Research Competition 2019 at the University of Alberta.

Black hole surface pop

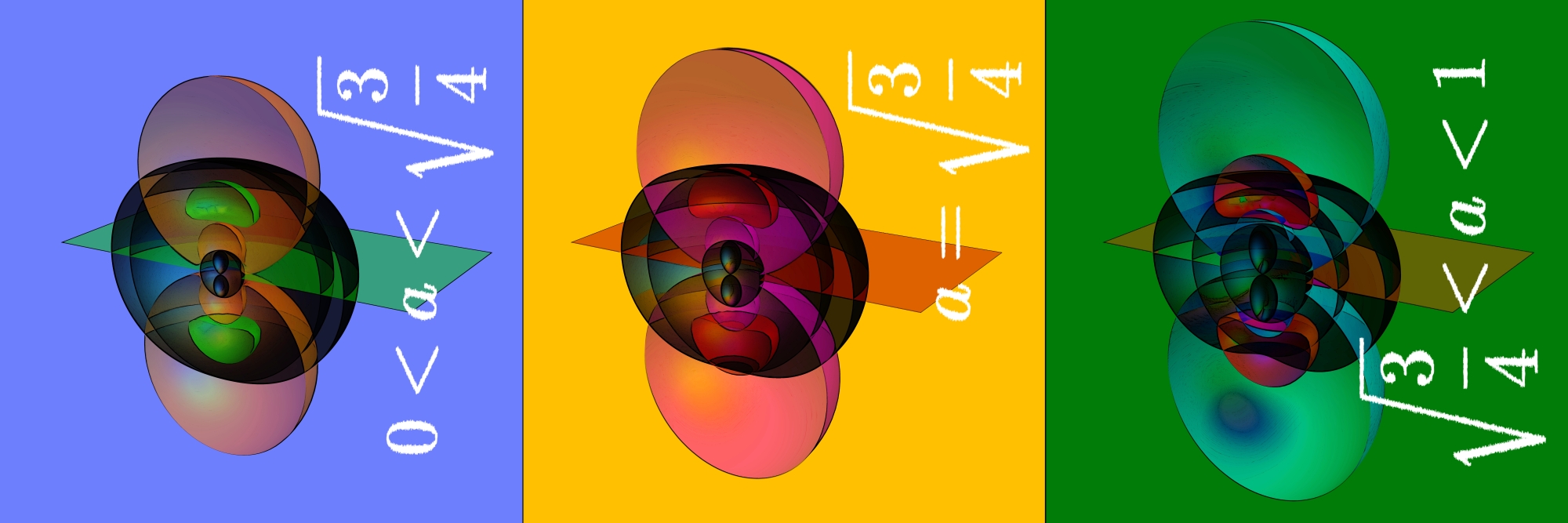
• Black holes belong to the most fascinating objects in our Universe, and they challenge the way we think about space and time. My research involves studying both mathematical and physical properties of black holes, and how they can help us to learn something new about the Universe we live in. With this contribution, I'm trying to bridge the gap between theoretical physics and modern art by mixing scientific results and the concept of pop art.
• My image contains three computer-generated plots of a rotating black hole, where the rotation speed “a” increases from left to right. The black surfaces correspond to the various horizons (the “membranes,” that once you pass them, you can never get out again). The other surfaces have a more involved meaning, in that they visualize the vanishing of so-called curvature invariants.
• Look at the green lobes in the leftmost picture, and track their shape as the rotation speed “a” increases to the right. In the middle one, for a critical value, they touch the horizon at the north and south pole, and in the right picture they protrude outside of the horizon. Mathematically it means that only for the first two pictures we can think of the black hole horizon as a surface in flat three-dimensional space, and not for the third one.
• Based on J.B. and A. Favaro, “Kerr principal null directions from Bel–Robinson and Kummer surfaces,” arXiv:1703.10791 [gr-qc]. My contribution to the Images of Research Competition 2018 at the University of Alberta, which received a semi-finalist prize.

Press

A lot of my work in theoretical physics is inspired by the extreme physics inside of black holes, and what we can do to better understand them. In this interview I spoke with Joe McClain at William & Mary about some aspects of my work:

I wrote an invited article for the University of Alberta's YouAlberta news outlet, covering my experiences in graduate school, my research on black holes, and my outreach activities at the 3MT competition:

My PhD thesis “Effects of Non-locality in Gravity and Quantum Theory” was awarded the PR Wallace Thesis Prize of the Canadian Association of Physicists (Division of Theoretical Physics), and my alma mater interviewed me on this prize and my research in this article:

The University of Alberta selected me as one of their 2020 featured graduates to be covered in a small article, which you can find here:

After receiving the prestigious Vanier Canada Graduate Scholarship in 2017 I was interviewed about my graduate research and my general interest in physics. See the article here: